Limit Trigonometri
Nama : Wellyan Fionaris
Mahasiswa : IT-PLN
HALOOOO! materi kali ini tentang limit trigonometri yaa. nah, untuk contoh soal lebih lanjut, bisa lihat di YT aku yaa! @wellyanfionaris
semoga membantu!
Limit Trigonometri
*pengertian :
-> limit fungsi trigonometriadalah limit yang fungsi terdiri dari variabel dan fungsi trigonometri, atau nilai terdekat suatu sudut pada fungsi trigonometri. Perhitungan limit fungsi trigonometri bisa langsung disubtitusikan seperti limit fungsi aljabar tetapi ada fungsi trigonometri yang harus diubah terlebih dahulu ke identitas trigonometri Contohnya:



Mahasiswa : IT-PLN
HALOOOO! materi kali ini tentang limit trigonometri yaa. nah, untuk contoh soal lebih lanjut, bisa lihat di YT aku yaa! @wellyanfionaris
semoga membantu!
Limit Trigonometri
*pengertian :
-> limit fungsi trigonometriadalah limit yang fungsi terdiri dari variabel dan fungsi trigonometri, atau nilai terdekat suatu sudut pada fungsi trigonometri. Perhitungan limit fungsi trigonometri bisa langsung disubtitusikan seperti limit fungsi aljabar tetapi ada fungsi trigonometri yang harus diubah terlebih dahulu ke identitas trigonometri Contohnya:

berikut strategi atau cara dalam menjawab soal trigonometri :
a. Strategi substitusi langsung

b. Strategi faktorisasi
Jika dari hasil substitusi langsung diperoleh nilai bentuk tak tentu, maka kita harus memfaktorkannya sehingga bentuknya menjadi bukan bentuk tak tentu, kemudian kita gunakan strategi substitusi langsung sehingga diperoleh hasilnya.
c. Strategi mengalikan dengan bentuk sekawan
Strategi mengalikan dengan bentuk sekawan dilakukan pada limit bentuk irasional. Ini dilakukan setelah sebelumnya kita menggunakan strategi substitusi langsung menghasilkan bentuk tak tentu. Setelah perkalian itu disederhanakan, kita menggunakan strategi substitusi langsung lagi, sehingga diperoleh hasilnya.
Cara biasa (rumus dasar limit fungsi trigonometri)
a. Fungsi Sinus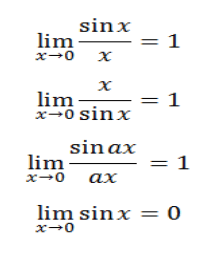
b. Fungsi Cosinus
c. Fungsi Tangen
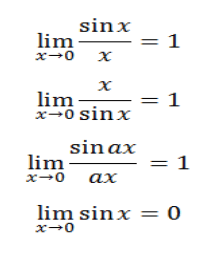
b. Fungsi Cosinus

c. Fungsi Tangen

2) Rumus Super
a. Tipe 1: Hubungan Sinus dan Tangen
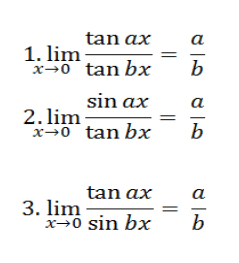
b. Tipe 2: Perkalian Sinus dan Tangen

c. Tipe 3: Hubungan Cosinus dan Sinus
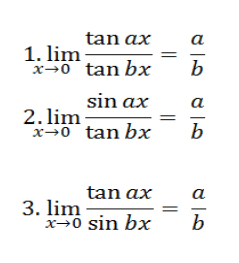
b. Tipe 2: Perkalian Sinus dan Tangen

c. Tipe 3: Hubungan Cosinus dan Sinus




Komentar
Posting Komentar