Matrik invers - Metode Adjoint dan OBE
Halooo Sobat Tematik!
Bagaimana kabaranya? Semoga sehat selalu yaa! aamiin
Nah, di Blog kali ini kita akan masuk ke materi invers matrik. Metode kali ini adalah metode Adjoint dan OBE. cussss ke materi ↓↓↓
Invers Matriks
Matriks yang memiliki invers disebut : nonsingular
Matriks yang tidak memiliki invers disebut : singular
Sebelumnya, Kita harus tahu jika bentuk sebuah invers matrik itu dilambangkan dengan Huruf kapital yang dipangkatkan -1 . contoh nama matriksnya adalah matriks A, maka invers dari matriks A biasa ditulis A-1 .
rumus invers matriks bisa dilihat di bawah ini :
a. A =
* Invers Matriks berordo 3x3
untuk mencari invers matriks berordo 3x3 bisa menggunakan metode-metode berikut
1. Metode Adjoint
Adjoin A dirumuskan sebagai berikut.
 "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
contoh soal:
2.Dengan Transformasi Baris Elementer
* untuk mencari b2,b3 >> lawan dari angka(misalkan positif (+) menjadi negatif (-)
Bagaimana kabaranya? Semoga sehat selalu yaa! aamiin
Nah, di Blog kali ini kita akan masuk ke materi invers matrik. Metode kali ini adalah metode Adjoint dan OBE. cussss ke materi ↓↓↓
Invers Matriks
Matriks yang memiliki invers disebut : nonsingular
Matriks yang tidak memiliki invers disebut : singular
Sebelumnya, Kita harus tahu jika bentuk sebuah invers matrik itu dilambangkan dengan Huruf kapital yang dipangkatkan -1 . contoh nama matriksnya adalah matriks A, maka invers dari matriks A biasa ditulis A-1 .
rumus invers matriks bisa dilihat di bawah ini :
Keterangan :
A-1 : Invers Matriks (A)
Det (A) : Determinan Matriks (A)
Adj (A) : Adjoin Matriks (A)
* Invers Matriks berordo 2x2
Untuk mencari invers matrik berordo 2x2, dapat menggunakan rumus berikut:
Jika 
maka matriks tersebut tidak mempunyai invers, atau disebut matriks singular.
maka matriks tersebut tidak mempunyai invers, atau disebut matriks singular.
Sifat-sifat matriks persegi yang mempunyai invers:
%5E%7B-1%7D+%3D+B%5E%7B-1%7D+%5Ccdot+A%5E%7B-1%7D&bg=T&fg=000000&s=0 "(A \cdot B)^{-1} = B^{-1} \cdot A^{-1}")
%5E%7B-1%7D+%3D+A%5E%7B-1%7D+%5Ccdot+B%5E%7B-1%7D&bg=T&fg=000000&s=0 "(B \cdot A)^{-1} = A^{-1} \cdot B^{-1}")
%5Et+%3D(A%5E%7Bt%7D)%5E%7B-1%7D&bg=T&fg=000000&s=0 "(A^{-1})^t =(A^{t})^{-1}")
Contoh soal:
Tentukan invers matriks-matriks berikut.
a. A =
b. B = 
Jawaban:
* Invers Matriks berordo 3x3
untuk mencari invers matriks berordo 3x3 bisa menggunakan metode-metode berikut
1. Metode Adjoint
adjoin A dinotasikan adj (A), yaitu transpose dari matriks yang elemen-elemennya merupakan kofaktor-kofaktor dari elemen-elemen matriks A, yaitu :
adj(A) = (kof(A))T
Adjoin A dirumuskan sebagai berikut.
Invers matriks persegi berordo 3 × 3 dirumuskan sebagai berikut.
contoh soal:
Carilah invers matriks dari matriks ordo 3x3 berikut ini :
1. Langkah pertama mencari matriks kofaktornya :
2. Langkah berikutnya adalah mencari matriks ADJOIN nya :
Maka matriks adjoin nya menjadi :
3. Langkah ketiga mencari determinan dari matriks A:
4. Langkah terakhir adalah mencari invers matriksnya :
Maka matriknya menjadi :
A =
|
1. Langkah pertama mencari matriks kofaktornya :
Kof A =
|
Kof A =
|
2. Langkah berikutnya adalah mencari matriks ADJOIN nya :
Kof A =
|
Maka matriks adjoin nya menjadi :
Matriks Adj A =
|
3. Langkah ketiga mencari determinan dari matriks A:
det(A) =
|
|
det(A) = (3.1.2)+(1.1.6)+(0.2.2)-(0.1.6)-(3.1.2)-(1.2.2)
= 6 + 6 + 0 - 0 - 6 - 4
= 24. Langkah terakhir adalah mencari invers matriksnya :
A-1= 12
|
Maka matriknya menjadi :
A-1=
|
2.Dengan Transformasi Baris Elementer
Ada 3 cara pada metode ini :
- Menukar 1 baris dengan baris yang lain
- Mengalikan sebuah baris dengan sebuah bilangan bukan 0
- Menjumlahkan kelipatan sebuah baris dengan baris yang lain
Notasi yang sering digunakan dalam transformasi baris elementer adalah :
a) Bi ↔ Bj : menukar elemen-elemen baris ke-i dengan elemen-elemen baris ke-j;
b) k.Bi : mengalikan elemen-elemen baris ke-i dengan skalar k;
c) Bi + kBj : jumlahkan elemen-elemen baris ke-i dengan k kali elemen-elemen baris ke-j.
contoh soal:
contoh soal:
penyelesaian:
ubah matriks sebelah kiri menjadi matriks identintas, dan matriks sebelah kanan menjadi isi dari invers matriks.
ubah matriks sebelah kiri menjadi matriks identintas, dan matriks sebelah kanan menjadi isi dari invers matriks.
dari penyelesaian diatas, terdapat 9 step penyelesaian. Kalikan sebaris bilangan matriks dengan rumus yang telah kita buat. jangan lupa, terdapat 3 cara pada metode OBE. silahkah gunakan salah satu mana yang tepat.
sekian, semoga bermaanfaat. maaf apa bila banyak kekurangan💗
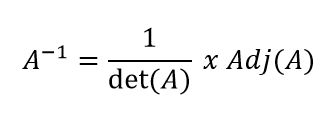
Komentar
Posting Komentar