Sistem Persamaan Linear - Metode Eliminasi Gauss dan Metode cramer

halooooooo sobat! 
Nah sekarang kita masuk ke materi baru, yaitu Sistem Persamaan Linear. Materi nya hampir sama dengan materi diwaktu kita duduk dibangku SMA dulu, tentu pasti ada yang beda bukan. Pada bangku perkuliahan ini kita sudah mulai dikenalkan dengan berbagai macam cara atau metode menghitung SPL.Sesuai judulnya, kali ini kita akan membahas metode eliminasi gauss dan crammer. apa itu? yukkk simak materinyaaaaa

Metode Eliminasi Gauss
Eliminasi Gauss adalah suatu metode untuk mengoperasikan nilai-nilai di dalam matriks sehingga menjadi matriks yang lebih sederhana lagi. Dengan melakukan operasi baris sehingga matriks tersebut menjadi matriks yang baris. Ini dapat digunakan sebagai salah satu metode penyelesaian persamaan linear dengan menggunakan matriks. Caranya dengan mengubah persamaan linear tersebut ke dalam matriks teraugmentasi dan mengoperasikannya. Setelah menjadi matriks baris, lakukan substitusi balik untuk mendapatkan nilai dari variabel-variabel tersebut.

Ciri ciri Metode Gauss adalah 
  1. Jika suatu baris tidak semua nol, maka bilangan pertama yang tidak nol adalah 1 (1 utama)
  2. Baris nol terletak paling bawah 
  3. 1 utama baris berikutnya berada dikanan 1 utama baris diatasnya
  4. Dibawah 1 utama harus nol

Pada metode gauss terdapat pengembangannya yakni Metode Gauss Jordan yang hasilnya lebih sederhana lagi. Caranya adalah dengan meneruskan operasi baris dari eliminasi Gauss sehingga menghasilkan matriks yang Eselon-baris. Ini juga dapat digunakan sebagai salah satu metode penyelesaian persamaan linear dengan menggunakan matriks.
Metode ini digunakan untuk mencari invers dari sebuah matriks.
Prosedur umum untuk metode eliminasi Gauss-Jordan ini adalah
1. Ubah sistem persamaan linier yang ingin dihitung menjadi matriks augmentasi.
2. Lakukan operasi baris elementer pada matriks augmentasi (A|b) untuk mengubah matriks
   A menjadi dalam bentuk baris eselon yang tereduksi


contoh soal untuk metode gauss
Tentukan nilai a,b,c,dan d dari sistem persamaan linear berikut menggunakan eliminasi gauss
2a - b + 3c - d = 11
-a + 2b - c - d = -4
3a + 3b + c + 3d = -2
-2a + 2b - 2c + 2d = 4
penyelesaian:
1. tahap pertama, ubah  sistem persamaan linear ke bentuk matriks, dan kerjakan seperti OBE (rubah ke bentuk matriks identintas)

seperti ini:
beri rumus atau formula pada setiap baris:













































Nah jika sudah begini, kita ketahui nilai dari x4 atau d = 27/4 = 6.75

2. Untuk mengetahui nilai x3 atau c, x2 atau b, dan x1 atau a adalah dengan subtitusikan persamaan


selesai. mudah bukan?
untuk penjelasan lebih lanjutnya silahkan tonton video youtube: wellyanfionaris yaaaa!
semoga membantuu


Metode Cramer
kaidah Cramer adalah rumus yang dapat digunakan untuk menyelesaikan sistem persamaan linear. Metode ini menggunakan determinan suatu matriks dan matriks lain yang diperoleh dengan mengganti salah satu kolom dengan vektor yang terdiri dari angka di sebelah kanan persamaannya. Metode ini dinamai dari matematikawan Swiss Gabriel Cramer (1704–1752)
Kaidah Cramer tidak efisien untuk sistem dengan lebih dari dua atau tiga persamaan.[1] Kaidah Cramer juga tidak stabil secara numerik, termasuk untuk sistem 2×2.[2]

Selesaikan sistem berikut dengan menggunakan aturan Cramer.
Contoh 2
Pembahasan Pertama kita tentukan determinan dari matriks koefisien untuk memastikan apakah aturan Cramer dapat diterapkan atau tidak. Dengan menggunakan baris ketiga kita mendapatkan
Contoh 2 D
Karena D ≠ 0, kita lanjut untuk menentukan determinan dari matriks-matriks lainnya dengan menggunakan Ms. Excel (rumus untuk menentukan determinan dalam Ms. Excel adalah “=MDETERM(array)”).
Contoh 2 Dx, Dy, Dz
Sehingga kita memperoleh,
Contoh 2 x, y, z
Jadi, selesaian dari sistem tersebut adalah (2, 0, –1). Selesaian ini dapat diuji ke dalam sistem yang diberikan. Semoga bermanfaat yaaa






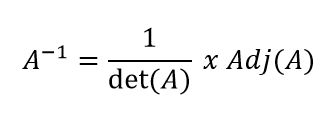
Komentar

Posting Komentar

Postingan populer dari blog ini

Matrik invers - Metode Adjoint dan OBE

Gambar
Halooo Sobat Tematik! Bagaimana kabaranya? Semoga sehat selalu yaa! aamiin Nah, di Blog kali ini kita akan masuk ke materi invers matrik. Metode kali ini adalah metode Adjoint dan OBE. cussss ke materi ↓↓↓ Invers Matriks        Matriks yang memiliki invers disebut : nonsingular        Matriks yang tidak memiliki invers disebut : singular Sebelumnya, Kita harus tahu jika bentuk sebuah invers matrik itu dilambangkan dengan Huruf kapital yang dipangkatkan -1 .  contoh nama matriksnya adalah matriks A, maka invers dari matriks A biasa ditulis  A -1   .     rumus invers matriks  bisa dilihat di bawah ini : Keterangan : A-1         : Invers Matriks (A) Det (A)   : Determinan Matriks (A) Adj (A)  : Adjoin Matriks (A) * Invers Matriks berordo 2x2  Untuk mencari invers matrik berordo 2x2, dapat menggunakan rumus berikut:    Ji...
Baca selengkapnya

Aljabar Linear- Basis dan Dimensi

BASIS DAN DIMENSI * Defenisi Umum Pengertian basis untuk ruang vektor V serupa dengan pengertian basis untuk R n , yang telah kita kenal. Untuk mengenal basis, diperlukan pengertian membangun dan bebas linier. Pengertian membangun telah kita pelajari di materi sebelumnya yaitu  kombinasi,bergantung, dan bebas linier  . Dengan pengertian bebas linier, himpunan yang membangun V dapat diperkecil sedemikian mungkin sehingga himpunan yang baru tetap membangun V. * contoh  Basis : suatu ukuran tertentu yang menyatakan komponen dari sebuah vector. Dimensi biasanya dihubungkan dengan ruang , misalnya garis adalah ruang dengan dimensi 1, bidang adalah uang dengan dimensi 2 dan seterusnya. Definisi basis secara umum adalah sebagai berikut : Jika V adalah ruang vektor dan S = {v1, v2, v3, ….., vn} adalah kumpulan vektor di dalam V, maka S disebut sebagai basis dari ruang vektor V jika 2 syarat berikut ini dipenuhi : i. S bebas linier; ii. S serentang ...
Baca selengkapnya

Limit bilangan Euler

Nama    :  Wellyan Fionaris Kampus : Mahasiswa IT-PLN Haloo semua! nah materi kali ini kita membahas tentang limit khusus, yakni bilangan euler. o iyaa, walaupun belajar dirumah, tetap stay safe yaa manteman 💓  Pengertian Limit Euler          Barisan  bilangan dapat dianggap sebagai fungsi dengan domain  bilangan asli . Misalkan diberikan fungsi f ( n ) = ( 1 + 1 n ) n f ( n ) = ( 1 + 1 n ) n dengan  n n   bilangan asli . Rumus fungsi tersebut dapat dikembangkan dengan menerapkan  Ekspansi Newton , yaitu ( 1 + 1 n ) n = C n 0 + C n 1 ( 1 n ) + C n 2 ( 2 n ) 2 + C n 3 ( 3 n ) 3 + ⋯ = 1 + n ( 1 n ) + n ( n − 1 ) 2 ! ⋅ n 2 + n ( n − 1 ) ( n − 2 ) 3 ! ⋅ n 3 + ⋯ ( 1 + 1 n ) n = C 0 n + C 1 n ( 1 n ) + C 2 n ( 2 n ) 2 + C 3 n ( 3 n ) 3 + ⋯ = 1 + n ( 1 n ) + n ( n − 1 ) 2 ! ⋅ n 2 + n ( n − 1 ) ( n − 2 ) 3 ! ⋅ n 3 + ⋯ Untuk  n → ∞ n → ∞ , ditulis lim n → ∞ ( 1 + 1 n ) n = 1 + 1 + 1 2 ! + 1 3 ! + 1 4 ! +...
Baca selengkapnya