SIFAT-SIFAT DETERMINAN MATRIKS 1

Haloo! pada blog kali ini kita masih bahas tentang matriks yaa, lebih tepatnya Sifat-sifat Determinan Matriks. cuusss ke materi ↓↓↓↓↓


Sifat-sifat Determinan Matriks :

Sifat 1

Jika matriks A$A$ dan B$B$ adalah matriks persegi yang berordo sama maka

det(AB)=det(BA)=det(A)×det(B)$$\boxed{{\displaystyle \text{det}(AB)=\text{det}(BA)=\text{det}(A)\times \text{det}(B)}}$$

Contoh 1

MIsalkan A,B$A,B$ dan C$C$ adalah matriks persegi yang mempunyai ordo yang sama, dengan C=AB$C=AB$.

A=[−3012], B=[2−4−35]$$A=\left[\begin{array}{cc}-3& 1\\ 0& 2\end{array}\right],B=\left[\begin{array}{cc}2& -3\\ -4& 5\end{array}\right]$$

Tentukan determinan dari matriks C$C$.

Penyelesaian :

Cara pertama, kita lakukan operasi perkalian matriks, sehingga didapat :

C=AB=[−3012][2−4−35]=[−6−40−89+50+10]=[−10−81410]$$\begin{array}{rl}C& =AB\\ & =\left[\begin{array}{cc}-3& 1\\ 0& 2\end{array}\right]\left[\begin{array}{cc}2& -3\\ -4& 5\end{array}\right]\\ & =\left[\begin{array}{cc}-6-4& 9+5\\ 0-8& 0+10\end{array}\right]\\ & =\left[\begin{array}{cc}-10& 14\\ -8& 10\end{array}\right]\end{array}$$

Kemudian kita hitung determinan dari matriks C$C$

det(C)=∣∣∣−10−81410∣∣∣=−100−(−112)=12$$\begin{array}{rl}\text{det}(C)& =\left|\begin{array}{cc}-10& 14\\ -8& 10\end{array}\right|\\ & =-100-(-112)\\ & =12\end{array}$$

Cara kedua, kita gunakan sifat 1, sehingga

det(C)=det(AB)=det(A)×det(B)=∣∣∣−3012∣∣∣×∣∣∣2−4−35∣∣∣=−6×(−2)=12$$\begin{array}{rl}\text{det}(C)& =\text{det}(AB)\\ & =\text{det}(A)\times \text{det}(B)\\ & =\left|\begin{array}{cc}-3& 1\\ 0& 2\end{array}\right|\times \left|\begin{array}{cc}2& -3\\ -4& 5\end{array}\right|\\ & =-6\times (-2)\\ & =12\end{array}$$

Setelah kita amati ternyata dua cara di atas mempunyai hasil akhir yang sama, namun dari segi efisiensi lebih baik cara kedua.

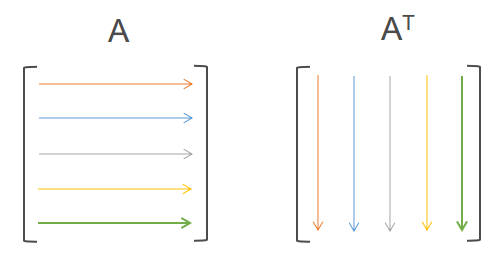
Sifat 2

Jika A$A$ adalah matriks persegi dan AT$A^T$ adalah transpose matriks A$A$, maka berlaku

det(A)=det(AT)$$\boxed{{\displaystyle \text{det}(A)=\text{det}\left(A^T\right)}}$$

Contoh 2

Misalkan matriks A$A$ didefinisikan sebagai berikut :

A=[1324]$$A=\left[\begin{array}{cc}1& 2\\ 3& 4\end{array}\right]$$

Tentukanlah nilai dari det(AT)$\text{det}\left(A^T\right)$

Penyelesaian :

Cara pertama (manual) dengan mentranspose matriks A$A$

AT=[1234]$$A^T=\left[\begin{array}{cc}1& 3\\ 2& 4\end{array}\right]$$

Selanjutnya menghitung determinan dari AT$A^T$

det(AT)=∣∣∣1234∣∣∣=4−6=−2$$\begin{array}{rl}\text{det}\left(A^T\right)& =\left|\begin{array}{cc}1& 3\\ 2& 4\end{array}\right|\\ & =4-6\\ & =-2\end{array}$$

Cara kedua menggunakan sifat

det(AT)=det(A)=∣∣∣1324∣∣∣=4−6=−2$$\begin{array}{rl}\text{det}\left(A^T\right)& =\text{det}(A)\\ & =\left|\begin{array}{cc}1& 2\\ 3& 4\end{array}\right|\\ & =4-6\\ & =-2\end{array}$$

Sifat 3

Jika A adalah matriks diagonal atau matriks skalar, maka

det(A)=a11×a22×⋯×ann$$\boxed{{\displaystyle \text{det}(A)=a_{11}\times a_{22}\times \cdots \times a_{nn}}}$$

(Determinan A$A$ adalah perkalian semua entri pada diagonal utama)

Contoh 3

Diberikan matriks A$A$ sebagai berikut :

A=⎡⎣⎢2–√000−200012⎤⎦⎥$$A=\left[\begin{array}{ccc}\sqrt{2}& 0& 0\\ 0& -2& 0\\ 0& 0& \frac{1}{2}\end{array}\right]$$

Tentukan determinan matriks A$A$

Penyelesaian :

Cara pertama menggunakan aturan sarrus, atau dapat dituliskan :

⎡⎣⎢⎢2–√000−2000122–√000−20⎤⎦⎥⎥$$\left[\begin{array}{ccccc}\sqrt{2}& 0& 0& \sqrt{2}& 0\\ 0& -2& 0& 0& -2\\ 0& 0& \frac{1}{2}& 0& 0\end{array}\right]$$

sehingga determinan dari A$A$ yakni :

det(A)=−2–√+0+0−0−0−0=−2–√$$\begin{array}{rl}\text{det}(A)& =-\sqrt{2}+0+0-0-0-0\\ & =-\sqrt{2}\end{array}$$

Cara kedua dengan menggunakan sifat didapat :

det(A)=∣∣∣∣∣2–√000−200012∣∣∣∣∣=2–√×−2×12=−2–√$$\begin{array}{rl}\text{det}(A)& =\left|\begin{array}{ccc}\sqrt{2}& 0& 0\\ 0& -2& 0\\ 0& 0& \frac{1}{2}\end{array}\right|\\ & =\sqrt{2}\times -2\times \frac{1}{2}\\ & =-\sqrt{2}\end{array}$$

Sifat 4

Jika A$A$ adalah matriks segitiga (atas/bawah) maka

det(A)=a11×a22×⋯×ann$$\boxed{{\displaystyle \text{det}(A)=a_{11}\times a_{22}\times \cdots \times a_{nn}}}$$

(Determinan A$A$ adalah perkalian semua entri pada diagonal utama)

Contoh 4

Misalkan diberikan matriks A3×3=[aij]$A_{3\times 3}=[a_{ij}]$ sebagai berikut :

A=⎡⎣⎢⎢π003420−123–√32⎤⎦⎥⎥$$A=\left[\begin{array}{ccc}\pi & \frac{3}{4}& -1\\ 0& 2& 2\sqrt{3}\\ 0& 0& \frac{3}{2}\end{array}\right]$$

Tentukan determinan dari matriks A$A$

Penyelesaian :

Cara pertama : Jika pada contoh 3, kita telah menggunakan metode sarrus. Sekarang kita akan menggunakan metode ekspansi kofaktor pada kolom pertama (a11=π,a21=0,a31=0)$(a_{11}=\pi ,a_{21}=0,a_{31}=0)$.

det(A)=a11C11+a21C21+a31C31=a11C11=π(−1)1+1∣∣∣2023–√32∣∣∣=π(3−0)=3π$$\begin{array}{rl}\text{det}(A)& =a_{11}{C}_{11}+a_{21}{C}_{21}+a_{31}{C}_{31}\\ & =a_{11}{C}_{11}\\ & =\pi (-1{)}^{1+1}\left|\begin{array}{cc}2& 2\sqrt{3}\\ 0& \frac{3}{2}\end{array}\right|\\ & =\pi (3-0)\\ & =3\pi \end{array}$$

Cara kedua menggunakan sifat maka :

det(A)=a11×a22×a33=π×2×32=3π