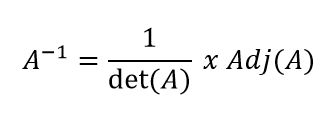SIFAT-SIFAT DETERMINAN MATRIKS (2)

Sifat 5

Jika A$A$ adalah matriks persegi berordo n×n$n\times n$ dan k$k$ adalah sebarang bilangan maka

det(kA)=kn×det(A)$$\boxed{{\displaystyle \text{det}(kA)=k^n\times \text{det}(A)}}$$

Contoh 5

Diketahui :

A=[2648]$$A=\left[\begin{array}{cc}2& 4\\ 6& 8\end{array}\right]$$

Tentukan determinan dari 3A$3A$

Penyelesaian :

Cara pertama, dengan mengalikan matriks A$A$ dengan 3 sehingga didapat :

3A=3×[2648]=[6181224]$$\begin{array}{rl}3A& =3\times \left[\begin{array}{cc}2& 4\\ 6& 8\end{array}\right]\\ & =\left[\begin{array}{cc}6& 12\\ 18& 24\end{array}\right]\end{array}$$

Kemudian kita hitung determinannya.

det(3A)=∣∣∣6181224∣∣∣=(6)(24)−(12)(18)=−72$$\begin{array}{rl}\text{det}(3A)& =\left|\begin{array}{cc}6& 12\\ 18& 24\end{array}\right|\\ & =(6)(24)-(12)(18)\\ & =-72\end{array}$$

Cara kedua dengan menggunakan sifat.

det(3A)=32×det(A)=9×∣∣∣2648∣∣∣=9(16−24)=−72$$\begin{array}{rl}\text{det}(3A)& =3^2\times \text{det}(A)\\ & =9\times \left|\begin{array}{cc}2& 4\\ 6& 8\end{array}\right|\\ & =9(16-24)\\ & =-72\end{array}$$

Sifat 6

Jika matriks A$A$ dapat dibalik (invertible) atau mempunyai invers, maka

det(A−1)=1det(A)$$\boxed{{\displaystyle \text{det}\left(A^{-1}\right)=\frac{1}{\text{det}(A)}}}$$

Contoh 6

Diketahui :

A=[−4213]$$A=\left[\begin{array}{cc}-4& 1\\ 2& 3\end{array}\right]$$

Tentukan nilai determinan dari A−1$A^{-1}$

Penyelesaian :

Cara pertama :

Umumnya pada saat kita mencari invers dari matriks A2×2=[aij]$A_{2\times 2}=[a_{ij}]$, kita menggunakan rumus :

A−1=1det(A)[a22−a21−a12a11]$$A^{-1}=\frac{1}{\text{det}(A)}\left[\begin{array}{cc}{a}_{22}& -a_{12}\\ -a_{21}& a_{11}\end{array}\right]$$

Sehingga berdasarkan rumus di atas kita dapatkan :

A−1=1−12−2[3−2−1−4]=[−314214114414]$$\begin{array}{rl}{A}^{-1}& =\frac{1}{-12-2}\left[\begin{array}{cc}3& -1\\ -2& -4\end{array}\right]\\ & =\left[\begin{array}{cc}-\frac{3}{14}& \frac{1}{14}\\ \frac{2}{14}& \frac{4}{14}\end{array}\right]\end{array}$$

Selanjutnya kita hitung determinan dari A−1$A^{-1}$.

det(A−1)=∣∣∣−314214114414∣∣∣=(−314)(414)−(114)(214)=−14196=−114$$\begin{array}{rl}\text{det}\left(A^{-1}\right)& =\left|\begin{array}{cc}-\frac{3}{14}& \frac{1}{14}\\ \frac{2}{14}& \frac{4}{14}\end{array}\right|\\ & =\left(-\frac{3}{14}\right)\left(\frac{4}{14}\right)-\left(\frac{1}{14}\right)\left(\frac{2}{14}\right)\\ & =\frac{-14}{196}\\ & =-\frac{1}{14}\end{array}$$

Cara kedua menggunakan sifat, kita peroleh :

det(A−1)=1det(A)=1−12−2=−114$$\begin{array}{rl}\text{det}\left(A^{-1}\right)& =\frac{1}{\text{det}\left(A\right)}\\ & =\frac{1}{-12-2}\\ & =-\frac{1}{14}\end{array}$$

Sifat 7

Jika A$A$ adalah matriks persegi yang memuat baris nol atau kolom nol maka

det(A)=0$$\boxed{{\displaystyle \text{det}(A)=0}}$$

Contoh 7

Misalkan matriks A$A$ dan B$B$ didefinisikan sebagai berikut :

A=⎡⎣⎢135000246⎤⎦⎥$$A=\left[\begin{array}{ccc}1& 0& 2\\ 3& 0& 4\\ 5& 0& 6\end{array}\right]$$

B=⎡⎣⎢520410300⎤⎦⎥$$B=\left[\begin{array}{ccc}5& 4& 3\\ 2& 1& 0\\ 0& 0& 0\end{array}\right]$$

Tentukan nilai determinan A$A$ dan B$B$

Pembuktian :

Cara pertama : dengan menggunakan metode ekspansi kofaktor, kita dapatkan :

det(A)=a12C12+a22C22+a32C32=(0)C12+(0)C22+(0)C32=0$$\begin{array}{rl}\text{det}(A)& =a_{12}{C}_{12}+a_{22}{C}_{22}+a_{32}{C}_{32}\\ & =(0)C_{12}+(0)C_{22}+(0)C_{32}\\ & =0\end{array}$$

(Ekspansi kofaktor sepanjang kolom kedua dari A$A$)

det(B)=b31C12+b32C22+b33C32=(0)C31+(0)C32+(0)C33=0$$\begin{array}{rl}\text{det}(B)& =b_{31}{C}_{12}+b_{32}{C}_{22}+b_{33}{C}_{32}\\ & =(0)C_{31}+(0)C_{32}+(0)C_{33}\\ & =0\end{array}$$

(Ekspansi kofaktor sepanjang baris ketiga dari B$B$)

Sifat 8

Jika A$A$ adalah matriks persegi dengan memuat dua baris yang saling berkelipatan atau dua kolom yang saling berkelipatan, maka

det(A)=0$$\boxed{{\displaystyle \text{det}(A)=0}}$$

Contoh 8

Tentukan determinan dari matriks berikut :

A=⎡⎣⎢−13−32−26153⎤⎦⎥$$A=\left[\begin{array}{ccc}-1& 2& 1\\ 3& -2& 5\\ -3& 6& 3\end{array}\right]$$

Penyelesaian :

Berdasarkan aturan sarrus maka :

⎡⎣⎢⎢−13−32−26153−13−32−26⎤⎦⎥⎥$$\left[\begin{array}{ccccc}-1& 2& 1& -1& 2\\ 3& -2& 5& 3& -2\\ -3& 6& 3& -3& 6\end{array}\right]$$

Sehingga diperoleh :

det(A)=(6)+(−30)+(18)−(6)−(−30)−(18)=0$$\begin{array}{rl}\text{det}(A)& =(6)+(-30)+(18)-(6)-(-30)-(18)\\ & =0\end{array}$$

Cara Alternatif yakni dengan memperhatikan baris-baris dan kolom-kolomnya, apabila terdapat dua baris atau dua kolomnya berkelipatan contohnya pada matriks A$A$, dimana baris ketiga merupakan kelipatan dari baris pertama. Sehingga berdasarkan sifat ke-8 ini maka det(A)=0$\text{det}(A)=0$.

Sifat 9

Contoh 9

Misalkan matriks A,B$A,B$ dan C$C$ didefinisikan sebagai berikut :

A=⎡⎣⎢151222−103⎤⎦⎥, B=⎡⎣⎢1−41232−113⎤⎦⎥, C=⎡⎣⎢111252−113⎤⎦⎥$$A=\left[\begin{array}{ccc}1& 2& -1\\ 5& 2& 0\\ 1& 2& 3\end{array}\right],B=\left[\begin{array}{ccc}1& 2& -1\\ -4& 3& 1\\ 1& 2& 3\end{array}\right],C=\left[\begin{array}{ccc}1& 2& -1\\ 1& 5& 1\\ 1& 2& 3\end{array}\right]$$

Kita akan mencoba memperlihatkan bahwa berdasarkan sifat ke-9 ini maka det(C)=det(A)+det(B)$\text{det}(C)=\text{det}(A)+\text{det}(B)$.

Pertama kita hitung nilai determinan dari matriks A,B$A,B$ dan C$C$.

det(A)=∣∣∣∣151222−103∣∣∣∣=−32$$\text{det}(A)=\left|\begin{array}{ccc}1& 2& -1\\ 5& 2& 0\\ 1& 2& 3\end{array}\right|=-32$$

det(B)=∣∣∣∣1−41232−113∣∣∣∣=44$$\text{det}(B)=\left|\begin{array}{ccc}1& 2& -1\\ -4& 3& 1\\ 1& 2& 3\end{array}\right|=44$$

det(C)=∣∣∣∣111252−113∣∣∣∣=12$$\text{det}(C)=\left|\begin{array}{ccc}1& 2& -1\\ 1& 5& 1\\ 1& 2& 3\end{array}\right|=12$$

Untuk cara perhitungannya bisa menggunakan aturan sarrus atau ekspansi kofaktor

DETERMINAN METODE CROUT DAN METODE DOOLITTLE

A. Metode Crout 

Untuk L = matriks segitiga atas, sedangkan U = segitiga bawah.

Rumus umum untuk mencari L dan U dengan Metode Crout : 

Dengan ordo 3x3 : 

Rumus perhitungannya :

B. Metode Doolittle

 Metode Doolittle berkebalikan dengan metode crout. Untuk L = segitiga bawah, dan untuk U = segitiga atas.

• Rumus umum untuk mencari L dan U dengan Metode Doolittle :

• Dengan ordo 3x3 :

Rumus perhitungannya: