Wellyan fionaris

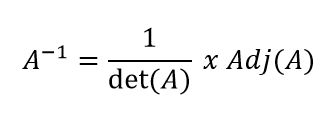
Halooo Sobat Tematik! Bagaimana kabaranya? Semoga sehat selalu yaa! aamiin Nah, di Blog kali ini kita akan masuk ke materi invers matrik. Metode kali ini adalah metode Adjoint dan OBE. cussss ke materi ↓↓↓ Invers Matriks        Matriks yang memiliki invers disebut : nonsingular        Matriks yang tidak memiliki invers disebut : singular Sebelumnya, Kita harus tahu jika bentuk sebuah invers matrik itu dilambangkan dengan Huruf kapital yang dipangkatkan -1 .  contoh nama matriksnya adalah matriks A, maka invers dari matriks A biasa ditulis  A -1   .     rumus invers matriks  bisa dilihat di bawah ini : Keterangan : A-1         : Invers Matriks (A) Det (A)   : Determinan Matriks (A) Adj (A)  : Adjoin Matriks (A) * Invers Matriks berordo 2x2  Untuk mencari invers matrik berordo 2x2, dapat menggunakan rumus berikut:    Ji...

Sifat 5 Jika  A A  adalah matriks persegi berordo  n × n n × n  dan  k k  adalah sebarang bilangan maka det ( k A ) = k n × det ( A ) det ( k A ) = k n × det ( A ) Contoh 5 Diketahui : A = [ 2 6 4 8 ] A = [ 2 4 6 8 ] Tentukan determinan dari  3 A 3 A Penyelesaian : Cara pertama, dengan mengalikan matriks  A A  dengan 3 sehingga didapat : 3 A = 3 × [ 2 6 4 8 ] = [ 6 18 12 24 ] 3 A = 3 × [ 2 4 6 8 ] = [ 6 12 18 24 ] Kemudian kita hitung determinannya. det ( 3 A ) = ∣ ∣ ∣ 6 18 12 24 ∣ ∣ ∣ = ( 6 ) ( 24 ) − ( 12 ) ( 18 ) = − 72 det ( 3 A ) = | 6 12 18 24 | = ( 6 ) ( 24 ) − ( 12 ) ( 18 ) = − 72 Cara kedua dengan menggunakan sifat. det ( 3 A ) = 3 2 × det ( A ) = 9 × ∣ ∣ ∣ 2 6 4 8 ∣ ∣ ∣ = 9 ( 16 − 24 ) = − 72 det ( 3 A ) = 3 2 × det ( A ) = 9 × | 2 4 6 8 | = 9 ( 16 − 24 ) = − 72 Sifat 6 Jika matriks  A A  dapat dibalik ( invertible ) atau mempunyai invers, maka det ( A − 1 ) = 1 det ( A ) de...